Vielog

如何利用 zk-snark 解决 Mental Poker 问题

Created on Sep 10, 2023

最近读到了几篇很有意思的文章, 讨论的是如何解决 Mental Poker 问题.

Mental poker 问题 是由 Rivest, Shamir and Adleman 三位密码学家于1979年提出 (就是 RSA 的那三位). 简单来讲, Mental Poker 问题可以理解为是在没有 “性感荷官” (一个 private 可信的第三方) 的场景下,进行扑克游戏. 下面的讨论我们将默认该 poker 游戏使用德州扑克的规则.

如何利用证明机制解决 Mental Poker 问题?

Geometry Research 基于论文 Mental Poker Revisited(Barnett and Smart, 2003) 中的协议, 提出了一个更为现代的解决方案[1]. 下文将形象的展示该方案是如何实现的.

Step One. Setup 阶段: 完成密码学相关设置

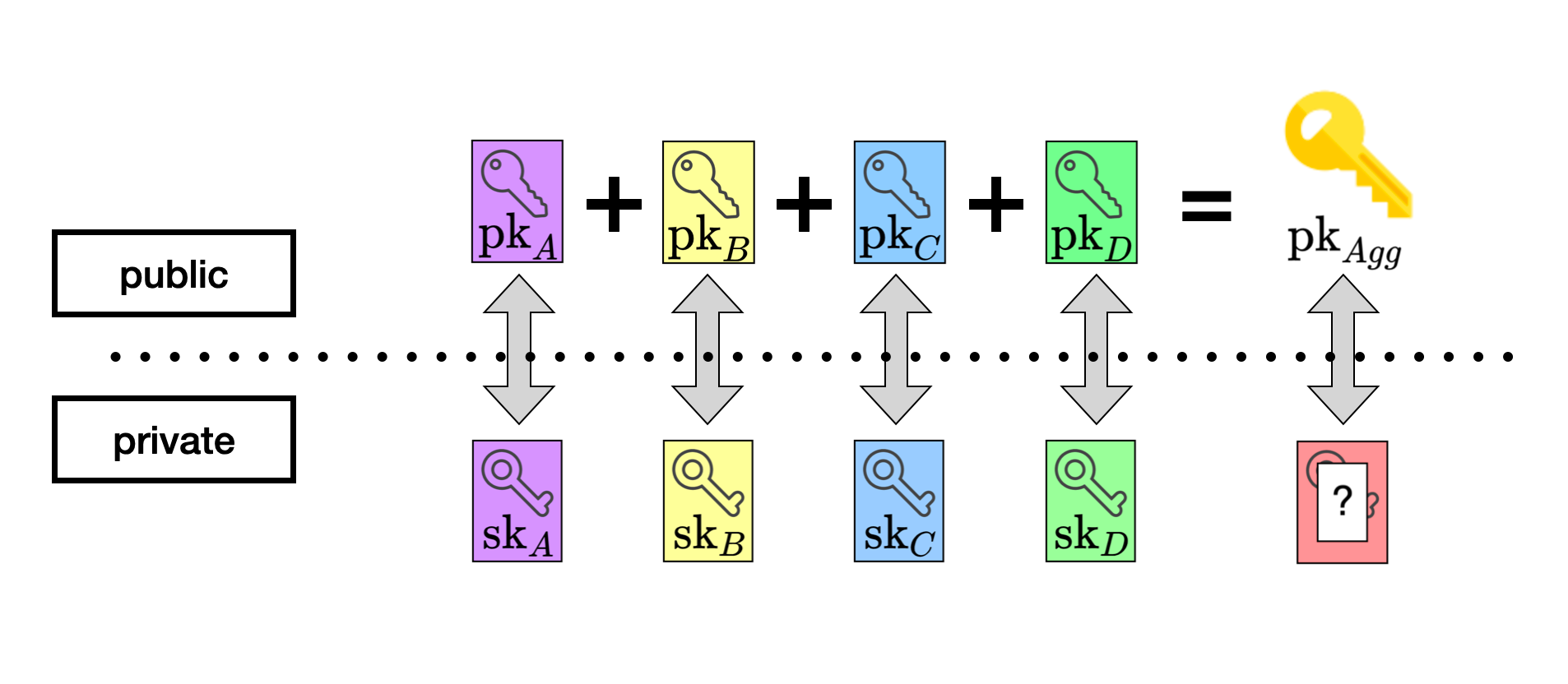
Setup keys

  • 每位玩家 i 生成自己的 公钥 pk_i, 私钥 sk_i, 所有 pk_i 聚合成一个 n-n 多签的 master_pk.
  • 所有玩家达成一个共识, 聚合产生一个公共的随机数 master_rand
  • 每位玩家 i 要发布一个证明, 证明对于用于聚合 master_pk 的 pk_i, 玩家 i 拥有相对应的 sk_i (Prove You Know Your Private Key). 该证明是用来防止恶意玩家发动 DoS attacks 和 Rogue Key attacks
  • 设置一个 public verifiable 的打乱函数Shuffle(list[], shuffle_nounce) -> shuffled_list[]), 该函数将根据 shuffle nounce 随机打乱一个有序列.

Step Two. Mask 阶段: 把牌翻过来

把扑克中 52 张牌(每一个牌面值为 m_i), 用 master_pk 和master_rand 进行 ElGamal 加密, 每张牌映射到到一密文(c1, c2) 上

  • mask(Card, mater_pk, master_rand) -> MaskedCard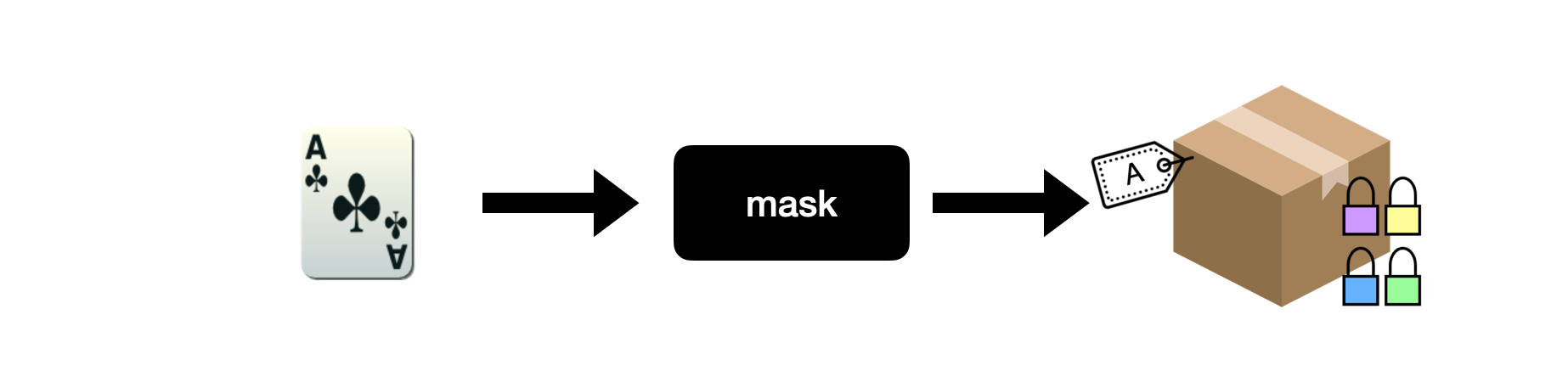mask cards
  • 进行 mask 操作的目的是把牌从字面值m_i, 映射到一组 elGamal 密文 field (c1, c2) 上, 方便后续进行洗牌. 所有玩家仍然知道 mask 过后的 card 对应的字面值.
  • mask 操作的执行者要发布一个 mask 操作的 validity proof, 向所有参与者证明自己 mask 的过程中没有作弊. (其他参与者当然可以自己执行 mask 操作, 直接检验 mask 结果是否一致).

Step Three. Shuffle and Remask 阶段: 把牌公平随机洗乱

洗牌过程中, 每一个玩家执行一次 shuffle_remask 操作, 每个玩家只知道自己洗的那次牌的前后映射关系, 每个人都洗一次保证了只有所有玩家通力合作才可以揭开洗完之后的牌. 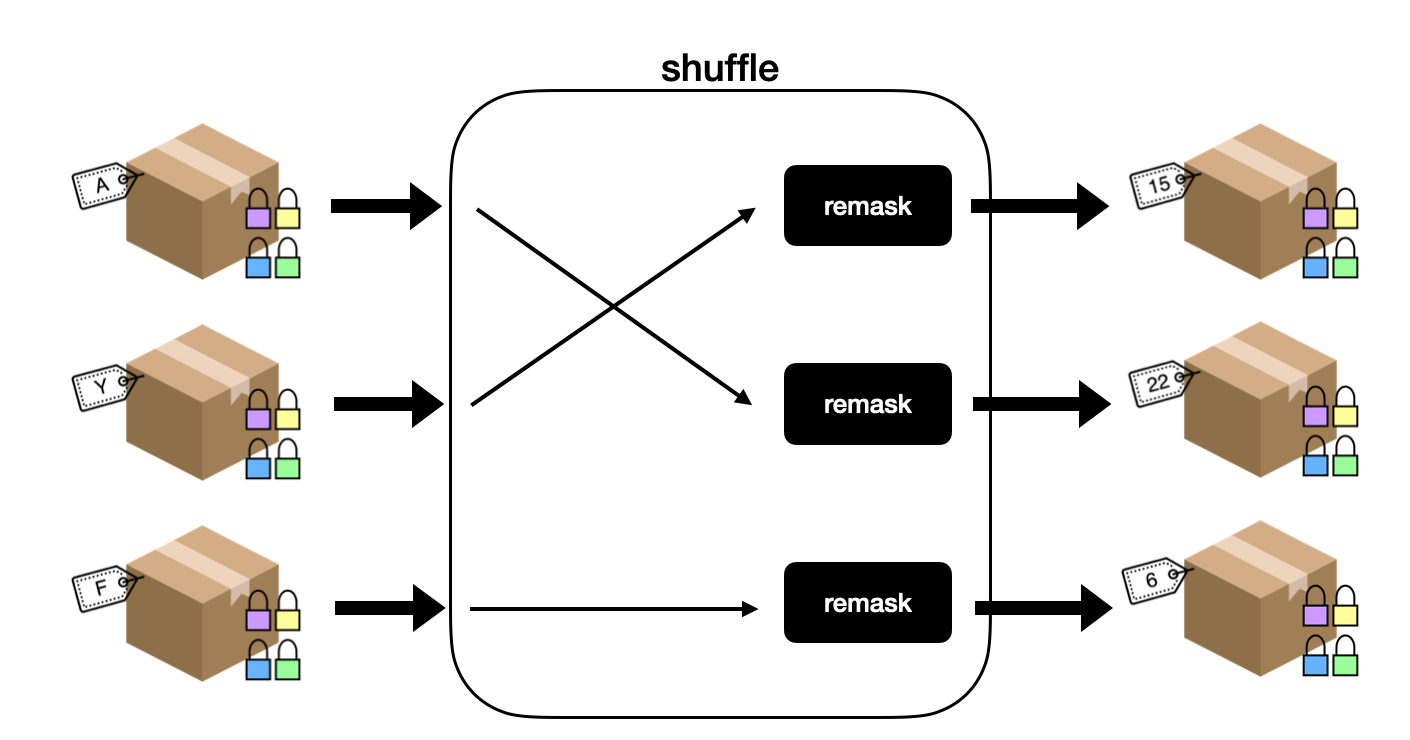shuffle

  • remask 操作: remask 操作和 mask 操作类似, 只是输入的类型字面值变为密文. 目的都是为了加密卡片的当前值. remask(MaskedCard, master_pk; rand) -> MaskedCard
    • 根据 remask 过程当中使用随机数和 master key, 能得到一个 reveal_token, 当一个经过所有玩家 remask 过的卡片 MaskedCard_i 只有被所有 reveal_token unmask 后才能揭开牌的牌面值 m_i.
  • shuffle_remask 操作:
    • 玩家先 pick 一个 random nounce 执行 shuffle 函数打乱接收到的牌序列.
    • 玩家在打乱之后, 再 pick 一个 randomness 把打乱后的每一张牌 remask 一次(同时生成对应的 reveal_token), 把 shuffle_remask 后的牌主组给下一个玩家, 直到所有玩家都洗过一遍.
  • 每位玩家要发布一个 shuffle_remask 操作的 zk validity proof (keep randomness secret), 向所有参与者证明 mask 的过程中没有作弊. 每个参与者都要验证其他所有人的洗牌操作.

Step Four. Reveal 阶段: 把牌发出去

根据前文所述的 unmask 操作, 所有玩家合作, 根据扑克规则, 给玩家发牌. 比如, 根据规则玩家一(拥有sk_1, pk_1, reveal_token_1) 应该得到牌堆的第一张牌masked_cards_1:

  • 除玩家一以外的所有玩家根据参与洗牌的顺序, 依次使用自己的 reveal_token unmask masked_cards_1, 最后将多次 unmask 的结果发送给玩家一, 玩家一最后再用自己的 reveal_token_1 unmask 一次, 得到牌的字面值 m_i.
  • 所有玩家在 unmask 是也要生成一个 unmask 操作的 validity proof, 确保牌被正确的 unmask. 其他玩家都要验证每一步的 unmask 过程, 防止部分玩家合作作弊.

Step Five: Compare 阶段: 比较手牌大小

在最后一个回合, 所有要求仍未棋牌玩家依次公开自己的手牌, 并证明自己的手牌是有效的. 玩家即可以通过公开并证明自己的 reveal token 揭示自己的手牌, 也可以自己 unmask 并公布牌面值, 并发布自己 unmask 操作的 validity proof.

总而言之, 根据我们前文所描述的内容, 在不涉及赌注结算的情况下, 我们可以在多个互相不信任的玩家之间实现 Mental Poker 游戏. 观察上面的协议, 我们可以很容易的发现, 一旦一个玩家不遵守游戏规则, 游戏就无法进行下去. 也就是说, 玩家可以轻易地发起 DoS attack.

如何在链上进行下注结算?

在讨论如何结算之前, 我们先要考虑以上针对 Mental Poker 的协议有那些特点:

  • 所有游戏的参与者相互不信任, 所有参与者通过 validity proof 相互验证操作, 确保其他玩家无法作弊.
  • 游戏能否进行下去取决于所有玩家是否都遵守规则: 即玩家应该根据协议, 在规定的回合完成自己应该完成的工作, 并向其他玩家证明自己工作的有效性.

了解了这两个特点, 我们可以进一步讨论如果我们想要在链上进行下注与结算, 安全目标有哪些?

  • 结算的公正性: 在 (n-1)/n 的玩家都尝试作弊的情况下, 结算层的胜负判定仍然是公正的.
    • 该目标的意义在于确保在每一局结算的时候, 结算结果的判定只取决于当前 Mental Pocker 协议的游戏规则与随机的洗牌的结果.
  • 底池的完整性: 一旦游戏开始, 任何一玩家(除非所有玩家都统一)都无法撤回投入底池当中的筹码, 底池保持其的单向流入直到结算.
  • 结算的必然性: 每局游戏都要根据游戏规则, 在一个固定时间上限以内公正地完成结算.
    • 在 Poker 游戏当中, 愿赌不一定服输, 处于劣势方的玩家有充分的动机阻止或是提前游戏的结算.
  • 游戏的完整性: 整个下注结算的过程要遵守 Mental Poker 的规则, 完成整个下注到结算的游戏过程.

下面我们将考虑不同安全目标下的设计思路:

情况一: 结算协议只要求保证结算的公正性. 我们可以轻松地在任何链上(evm, btc scripts)结合 n-n 多签以及可回退时间锁等技术实现结算合约. 该合约类似一个多方参与的 payment channel: 在一个结算时间之前各个子账户之间的资金分配操作通过 n-n 多签进行; 在结算时间后每个用户都可以拿回子账户的余额. 该合约显然保证了结算的公正性, 但是一旦玩家之间未能达成共识(出现了某些不遵守规则的玩家), 游戏将会中止, 最后资金按照终止前状态退还.

情况二: 只保证结算公正性与底池完整性, 结算层可以采取锁定底池的方式: 一旦玩家之间未达成共识, 结算层就锁定当前这一局的底池, 保证底池的完整性.

情况三: 满足前三个条件, 可以在方案一的基础上, 修改超时之后的结算规则. 这里有一个关键的知识, 即一场比赛的胜负在洗牌结束之后就已经确定了. 在共识无法达成触发超时结算的条件后, 结算层可以根据零知识证明等相关技术, 依据洗牌的时候提供的 commitments, 保证当前底池里面的余额仍划给胜利的一方. 但该设计未能满足游戏的完整性, 恶意玩家可以频繁的发动 DoS 攻击, 影响游戏体验.

情况四: 结算协议满足所有安全目标, 保证游戏完整的运行下去, 结算层需要识别出回合中不遵守规则的玩家. 游戏当中的每一步操作可以看作是一笔交易, 交易的顺序由游戏规则说确定)的 L2 (如果结算层是 L1 的话). 所有 L2 (玩家) 之间的操作具有时序先后关系, L1 需要根据游戏规则确定的顺序, 监督 L2 的操作. 因此, L2 为了向 L1 证明自己的正确性, 需要依照游戏周期, 向 L1 发送操作的 commitments/proofs.

我们可以参考 rollups 的设计思路, 大致也有两种解决方案:

  • 一种是类似于 op-rollups 基于欺诈证明的设计: 所有玩家在 L1 或是 DA 上打每一部操作的 commmitments, 其他玩家举证某个参与方的欺诈或是消极行为, 结算层接受并验证欺诈证明, 如果验证成功, 惩罚该作弊者(燃烧所有筹码等).
  • 一种是类似 zk-rollups 的 基于 validity proof 的设计, 结算层充当一个不参与游戏的玩家, 验证每一个玩家每一步的操作是否 valid. L2 可以通过 batch 等方式优化验证开销.

对比这两种实现方案, 前者的中, L2 完成大部分校验工作, L1 只需要在完成结算之前, 留下一些时间对可能提交欺诈证明进行校验, 在大多数情况下(所有参与者都是诚实的) L1 不需要验证. 而后者的方案, L1 需要完整校验所有玩家的所有操作, 有着更大的开销, 扩展性更差.

总结

基于近几十年的零知识证明技术在理论上工程实现上的快速进步, 在普通玩家的电脑上运行 Mental Poker 协议变得可行. 但为了完成在链上进行 Mental Poker 的结算, 结算层合约的设计者需要考虑结算安全指标与链上开销之间的平衡. 刚才上网找了找, zkholdem, 一个链上 Mental Poker Game 项目已经上了 testnet. 该项目非结算的部分与前文的思路基本一致, 但有关合约其实现的相关资料还比较少, 有时间再看看源码.

相关链接 本文第一部分主要参考以下链接:

  1. https://geometry.xyz/notebook/mental-poker-in-the-age-of-snarks-part-1
  2. https://geometry.xyz/notebook/mental-poker-in-the-age-of-snarks-part-2
  3. https://aandds.com/blog/schnorr-proof.html
  4. https://zkholdem.xyz/wp-content/themes/zkholdem-theme/zkshuffle.pdf

一些 Mental Poker 相关的库:

  1. https://github.com/geometryresearch/mental-poker
  2. https://github.com/kripod/mental-poker